Equilateral Triangle: Properties, Measurements, and Applications

What is an Equilateral Triangle?

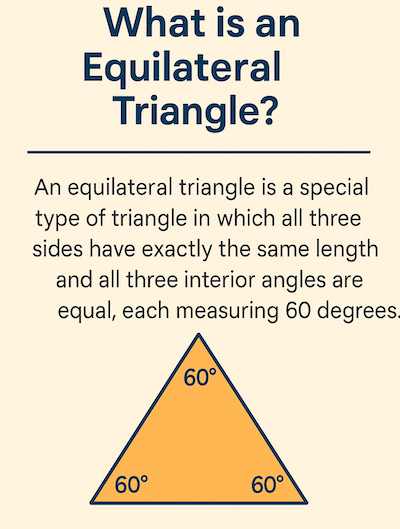
An equilateral triangle is a special type of triangle in which all three sides have exactly the same length and all three interior angles are equal, each measuring 60 degrees. The word “equilateral” itself tells us about this property – “equi” means equal and “lateral” refers to sides.

Because of this perfect symmetry, equilateral triangles possess several unique and interesting properties that make them important in mathematics, architecture, engineering, and design.

Key Properties of Equilateral Triangles

• All three sides have the same length
• All three interior angles equal 60°
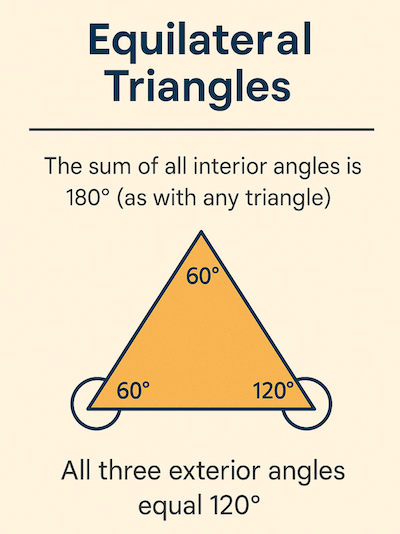
• The sum of all interior angles is 180° (as with any triangle)
• All three exterior angles equal 120°
• It has three lines of symmetry
• It has rotational symmetry of order 3
• The center of the triangle (where the three lines of symmetry intersect) is equidistant from all three vertices

How Many Lines of Symmetry Does an Equilateral Triangle Have?

An equilateral triangle has exactly three lines of symmetry. These are lines that pass through one vertex and the midpoint of the opposite side. If you fold the triangle along any of these three lines, the two halves will match perfectly.

This is one of the properties that makes the this triangle so special – it has the maximum possible number of lines of symmetry that any triangle can have. In comparison, an isosceles triangle has only one line of symmetry, and a scalene triangle has none.

Finding the Height of an Equilateral Triangle

The height of an this triangle is the perpendicular distance from any vertex to the opposite side. Due to the equal properties of the triangle, this height will be the same regardless of which vertex and opposite side you choose.

To find the height (h) of an equilateral triangle with side length s, we can use the Pythagorean theorem:

1. Draw the height from any vertex to the opposite side.
2. This creates a right triangle with:
   • Hypotenuse = s (the side length of the original triangle)
   • Base = s/2 (half the side length)
   • Height = h (what we’re trying to find)
3. Using the Pythagorean theorem: s² = (s/2)² + h²
4. Rearranging: h² = s² – (s/2)²
5. Simplifying: h² = s² – s²/4 = 3s²/4
6. Taking the square root: h = s√3/2

Therefore, the height of an equilateral triangle is: h = (s√3)/2

where s is the length of any side.

Finding the Area of an Equilateral Triangle

Now that we know how to find the height, calculating the area becomes straightforward. The area of any triangle can be found using the formula:

Area = (1/2) × base × height

For an equilateral triangle with side length s:

• Base = s
• Height = (s√3)/2

Therefore: Area = (1/2) × s × (s√3)/2 Area = (s² × √3)/4

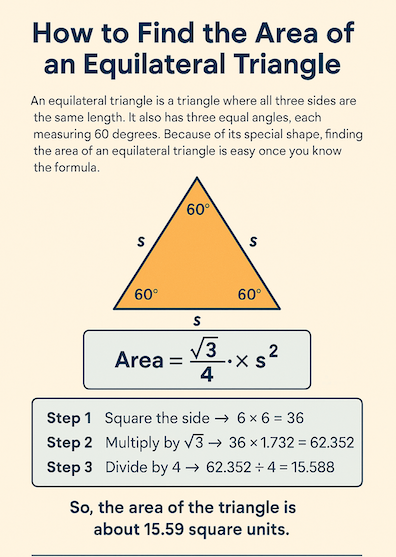
So the formula for the area of an equilateral triangle is: A = (s² × √3)/4

Example Problems and Solutions

Example 1: Finding the Height

Problem: An equilateral triangle has sides of length 8 cm. What is its height?

Solution: Using the formula h = (s√3)/2 h = (8 × √3)/2 h = 4√3 cm h ≈ 6.93 cm

Example 2: Finding the Area

Problem: An equilateral triangle has sides of length 10 m. What is its area?

Solution: Using the formula A = (s² × √3)/4 A = (10² × √3)/4 A = (100 × √3)/4 A = 25√3 m² A ≈ 43.3 m²

Example 3: Finding the Side Length from the Area

Problem: An equilateral triangle has an area of 36√3 cm². What is the length of each side?

Solution: We know that A = (s² × √3)/4 36√3 = (s² × √3)/4 36 × 4 = s² 144 = s² s = 12 cm

Applications of Equilateral Triangles

1. Architecture and Engineering: Equilateral triangles are used in truss designs because they create very stable structures.
2. Design and Art: They are often used in logos, patterns, and artistic compositions due to their aesthetic appeal and perfect symmetry.
3. Navigation: Triangulation methods often utilize properties of equilateral triangles.
4. Optics: Light passing through an equilateral triangular prism separates into the spectrum of colors.

Practice Questions

1. An equilateral triangle has a perimeter of 27 cm. What is the length of each side?
2. If the height of an equilateral triangle is 12 cm, what is the length of each side?
3. An equilateral triangle has an area of 16√3 cm². What is its height?
4. If an equilateral triangle has side length 6 units, what is its area?

Answers to Practice Questions

1. Since all sides are equal, and the perimeter is the sum of all sides: Perimeter = 3 × side length 27 = 3 × side length Side length = 9 cm
2. We know that height = (s√3)/2 12 = (s√3)/2 24 = s√3 24/√3 = s 24/√3 × √3/√3 = s 24√3/3 = s 8√3 ≈ 13.86 cm
3. Area = (s² × √3)/4 16√3 = (s² × √3)/4 64 = s² s = 8 cm Using h = (s√3)/2 h = (8√3)/2 h = 4√3 ≈ 6.93 cm
4. Area = (s² × √3)/4 Area = (6² × √3)/4 Area = (36 × √3)/4 Area = 9√3 ≈ 15.59 square unit